Moment of Inertia of a Triangle and How It Is Calculated

The moment of inertia is a crucial concept in physics and engineering that describes an object’s resistance to rotational motion. It plays a significant role in various fields, including mechanics, structural analysis, and dynamics.

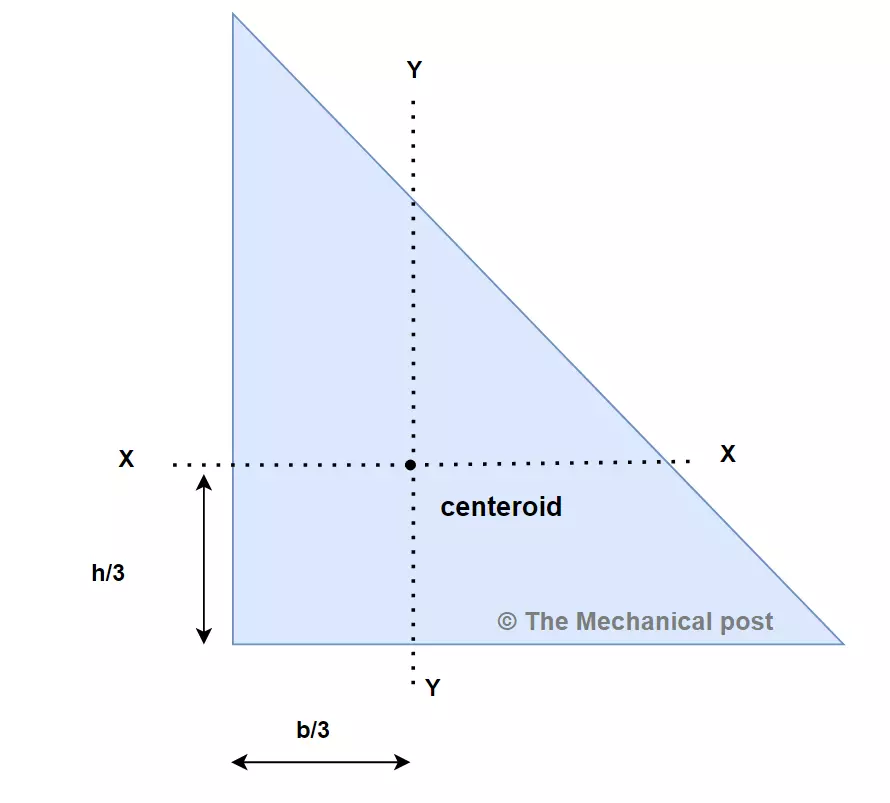
Triangle-moment-of-inertia
Moment of Inertia Calculator for Triangle
Your Answer is:
📋
📋

When it comes to calculating the moment of inertia of a triangle, it involves understanding the triangle’s geometry and applying relevant mathematical formulas. In this calculator tool, we will explore the concept of moment of inertia for a triangle and discuss how it can be calculated.

The unit of the answer is the same as the unit of the input dimension. Please make sure you enter all dimensions in same units.

.

Please Note:

Above values are calculated for a Right angle Triangle

.

Before delving into the calculation process, let’s understand what the moment of inertia represents. Essentially, it quantifies the distribution of mass around an axis of rotation. In simpler terms, it measures how the mass of an object is distributed concerning its rotation axis. For a triangle, the moment of inertia depends on its shape, dimensions, and the axis of rotation.

To calculate the moment of inertia of a triangle, we need to consider two perpendicular axes: the x-axis (Ix) and the y-axis (Iy). These axes pass through the centroid of the triangle, which is the point where the triangle’s medians intersect.

The moment of inertia values about these axes can provide valuable insights into the triangle’s rotational behavior.

To begin the calculation, we require two essential parameters: the base (b) and the height (h) of the triangle. The base refers to the length of the triangle’s bottom side, while the height represents the distance between the base and the opposite vertex. With these parameters, we can proceed to compute the moment of inertia.

For a triangle, the moment of inertia formulas differ depending on the axis of rotation. Let’s explore the calculations for both the x-axis (Ix) and the y-axis (Iy).

  1. Moment of Inertia about the x-axis (Ix):

Ix = (1/36) * b * h^3

This formula reveals that the moment of inertia about the x-axis is determined by multiplying the base length (b) by the cube of the height (h) and dividing the result by 36. The value obtained represents the triangle’s resistance to rotation around the x-axis.

  1. Moment of Inertia about the y-axis (Iy):

Iy = (1/36) * h * b^3

Similarly, the moment of inertia about the y-axis involves multiplying the height (h) by the cube of the base length (b) and dividing the result by 36. This value represents the triangle’s resistance to rotation around the y-axis.

Once we have calculated the moment of inertia values (Ix and Iy), we gain valuable information about the triangle’s rotational characteristics. These values help engineers and physicists understand how the triangle will behave when subjected to rotational forces or moments.

In addition to the moment of inertia, another important aspect of the triangle is its centroid. The centroid is the geometric center of the triangle and represents the point of balance. It divides each median into two segments in a 2:1 ratio, with the longer segment closer to the base. The coordinates of the centroid can be calculated as follows:

Centroid X = b/3
Centroid Y = h/3

These formulas determine the coordinates of the centroid based on the triangle’s base length (b) and height (h). The centroid provides crucial information about the triangle’s equilibrium and its behavior under various loading conditions.

Furthermore, it is also possible to calculate the area of the triangle using the base and height values. The formula for calculating the area is:

Area = (1/2) * b * h

By multiplying the base length (b) by the height (h) and dividing the result by 2, we obtain the area of the triangle. The area represents the region enclosed by the triangle’s sides

and provides insights into its size and spatial characteristics.

Conclusion:

When dealing with triangles, calculating the moment of inertia involves considering the triangle’s dimensions, shape, and axes of rotation. By applying the appropriate formulas, we can determine the moment of inertia values about the x-axis (Ix) and the y-axis (Iy), as well as the centroid and area of the triangle. These calculations provide valuable insights into the triangle’s rotational behavior and aid in designing structures and analyzing mechanical engineering systems.

Discover the latest in Mechanical Engineering field:

.